CS440/ECE448 Fall 2016

Assignment 1: Search

Due date: Monday, September 26, 11:59:59PM

Credits: Berkeley CS188 Pacman projects (Part 1), Manav Kedia and Kyo Hyun Kim (Part 2)

In this assignment, you will build general-purpose search algorithms and apply them to solving puzzles. In Part 1 (for everybody), you will be in charge of a "Pacman" agent that needs to find paths through mazes while eating one or more dots or "food pellets." In Part 2 (for four-credit students), you will tackle a simplified Rubik's Cube puzzle.

As stated in the beginning of the course, you are free to use any high-level programming language you are comfortable with. This includes (but is not limited to) Java, C++, Python, and MATLAB. The focus of this course is on problem solving, not programming, and the grading will primarily be based on the quality of your solutions and your analysis, as evidenced by your written report.

You have the option of working in groups of up to three people. Three-credit students must work with three-credit students and four-credit students must work with four-credit students. To form groups, feel free to use Piazza. Needless to say, working in a group will not necessarily make your life easier, as the overhead of group coordination can easily outweigh the benefits.

Contents

Part 1: For everybody

1.1 Basic pathfinding

Consider the problem of finding the shortest path from a given start state while eating one or more dots or "food pellets." The image at the top of this page illustrates the simple scenario of a single dot, which in this case can be viewed as the unique goal state. The maze layout will be given to you in a simple text format, where '%' stands for walls, 'P' for the starting position, and '.' for the dot(s) (see sample maze file). All step costs are equal to one.

Implement the state representation, transition model, and goal test needed for solving the problem in the general case of multiple dots. For the state representation, besides your current position in the maze, is there anything else you need to keep track of? For the goal test, keep in mind that in the case of multiple dots, the Pacman does not necessarily have a unique ending position. Next, implement a unified top-level search routine that can work with all of the following search strategies, as covered in class:

  • Depth-first search;
  • Breadth-first search;
  • Greedy best-first search;
  • A* search.
For this part of the assignment, use the Manhattan distance from the current position to the goal as the heuristic function for greedy and A* search.

Run each of the four search strategies on the following inputs:

For each problem instance and each search algorithm, include the following in your report:
  • The solution, displayed by putting a '.' in every maze square visited on the path.
  • The path cost of the solution, defined as the number of steps taken to get from the initial state to the goal state.
  • Number of nodes expanded by the search algorithm.

Part 1.2: Search with multiple dots

Now consider the harder problem of finding the shortest path through a maze while hitting multiple dots. Once again, the Pacman is initially at P, but now there is no single goal position. Instead, the goal is achieved whenever the Pacman manages to eat all the dots. Once again, we assume unit step costs.

As instructed in Part 1.1, your state representation, goal test, and transition model should already be adapted to deal with this scenario. The next challenge is to solve the following inputs using A* search using an admissible heuristic designed by you:

You should be able to handle the tiny search using uninformed BFS -- and in fact, it is a good idea to try that first for debugging purposes, to make sure your representation works with multiple dots. However, to successfully handle all the inputs, it is crucial to come up with a good heuristic. For full credit, your heuristic should be admissible and should permit you to find the solution for the medium search in a reasonable amount of time. In your report, explain the heuristic you chose, and discuss why it is admissible and whether it leads to an optimal solution.

For each maze, give the solution cost and the number of nodes expanded. Show your solution by numbering the dots in the order in which you reach them (once you run out of numbers, use lowercase letters, and if you run out of those, uppercase letters).

Part 1 extra credit: Suboptimal search

Sometimes, even with A* and a good heuristic, finding the optimal path through all the dots is hard. In these cases, we'd still like to find a reasonably good path, quickly. Write a suboptimal search algorithm that will do a good job on this big maze. Your algorithm could either be A* with a non-admissible heuristic, or something different altogether. In your report, discuss your approach and output the solution cost and number of expanded nodes. You don't have to show the solution path unless you want to come up with a nice animation for even more extra credit.

Tips

  • In your implementation, make sure you get all the bookkeeping right. This includes handling of repeated states (in particular, what happens when you find a better path to a state already on the frontier) and saving the optimal solution path. These topics have been extensively covered during the lectures.

  • Pay attention to tiebreaking. If you have multiple nodes on the frontier with the same minimum value of the evaluation function, the speed of your search and the quality of the solution may depend on which one you select for expansion.

  • Make sure you implement a unified top-level search algorithm that can take each of the four strategies as special cases. In particular, while DFS can be implemented very compactly using recursion, we want you to avoid this approach for the sake of the assignment (among other things, you can much more easily exceed the maximum depth of the recursion stack than if you explicitly represent the frontier as a stack).

  • In Part 1, you will be graded primarily on the correctness of your solution, not on the efficiency and elegance of your data structures. For example, we don't care whether your priority queue or repeated state detection uses brute-force search, as long as you end up expanding (roughly) the correct number of nodes and find the optimal solution. So, feel free to use "dumb" data structures as long as it makes your life easier and still enables you to find the solutions to all the inputs in a reasonable amount of time. However, in Part 2, you will have to handle repeated state detection more efficiently in order to successfully solve all the inputs.


Part 2 (For four-credit students): Rubik's Cube

Rubik's Cube has been a popular toy for nearly 40 years. In this part of the assignment, you will build a solver for a 2*2*2 "pocket cube," which is shown below. Please read both parts below and plan carefully before starting to code!

Part 2.1: Solving the Cube without Rotation Invariance

The cube has six faces: Top, Bottom, Front, Back, Left, and Right. Any one of its faces can be turned by 90 degrees in either the clockwise (CW) direction or the counterclockwise (CCW) direction. We denote the moves by a single capital letter for the face turned (Top, Bottom, Front, Back, Left, Right) and a prime mark if the face was turned CCW instead of CW. For example, the sequence of moves

T Bo Ba'

means turning the Top face clockwise followed by turning the Bottom face clockwise and finally turning the Back face counterclockwise. So your implementation should support these 12 types of moves.

There are six colors: red, green, blue, orange, yellow, and purple. We represent states or configurations of the cube by listing the colors in each of the four positions of each of the six faces. The cube is considered solved when each face has only one color and this configuration is reachable from the initial configuration.

The goal state used in this part of the assignment is as follows:

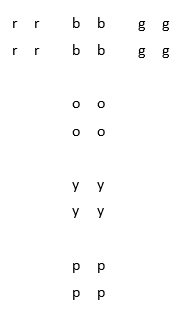
The face with 4 'r' is Left, the face with 4 'b' is Top, the face with 4 'g' is Right, the face with 4 'o' is Front, the face with 4 'y' is Bottom, and the face with 4 'p' is Back. The above configuration is the unique goal state for this part, i.e. for the cube to be considered solved the faces should have the colors as shown in the above diagram. No other state is to be considered as the goal even if the cube appears to be solved, i.e. has the same colors within each face.

More generally, for now, we DO NOT consider configurations to be the same if the entire cube can be rotated in space to go from one configuration to the other.

Here is a sample input in the same format as the goal state above:

Note that there are 4 spaces in the input files starting from the third line right up to the last line. Parse the input carefully according to this format specification.

The goal of this part is to solve the following three inputs with A* search: For the heuristic, consider the number of misplaced cubes. Is this heuristic admissible? Should it be multiplied or divided by a factor to make it admissible?

For each input, report the sequence of moves needed to reach the goal configuration using the move notation specified above. Also report the number of nodes expanded by your A* algorithm to find this solution, and the running time.

Tips

  • Be careful when implementing your transition model. For example, if you turn the front face in the clockwise direction, you should ensure that the blocks touching the blocks of the front face from the left, top, right, and bottom faces also move clockwise.

  • To have an efficient solution for Part 2, you need to use hashing for repeated state detection. In the report, describe your hashing strategy.

Part 2.2: Adding Rotation Invariance

If we consider the cube in 3D space, any two configurations that are separeted by a global 3D rotation are actually equivalent. In particular, we have 24 configurations that look different according to their 2D layout representation, but are actually equivalent in 3D (we can fix the front face in 6 ways and rotate the 4 sides attached to the front face in either clockwise or counter-clockwise direction 4 times). In this part, you need to modify your goal test, repeated state detection, and heuristic to take these equivalences into account. Describe the modifications in your report. With these modifications, you should be able to handle more complicated puzzles requiring longer solution paths. Run your modified A* search on the following inputs:
For each input, as before, give the solution path, the number of nodes expanded, and the running time. For the first input, discuss the differences between the solutions and the behavior of the two versions of your algorithm. If you run into running time or memory problems on any of the inputs, feel free to set a cutoff on the search depth or number of nodes expanded, and specify in your report at which point you had to terminate the search.

Part 2 Extra Credit

  • Try to come up with a better admissible heuristic. Explain why is it admissible. Compare the number of nodes expanded and running time for the two heuristics on the inputs above, and run A* search with this new heuristic on input 3.1.

  • Try to generate harder Rubik's Cube instances by applying some sequence of moves from the goal state. Try to find out the maximum depth of solution paths your code can handle. Report on your findings and observations.

  • Generate a 3D animation of your solutions and make a cool video. The video can either be included in the zip file or put on the Web, with a link from the report.

Report Checklist

Your report should briefly describe your implemented solution and fully answer the questions for every part of the assignment. Your description should focus on the most "interesting" aspects of your solution, i.e., any non-obvious implementation choices and parameter settings, and what you have found to be especially important for getting good performance. Feel free to include pseudocode or figures if they are needed to clarify your approach. Your report should be self-contained and it should (ideally) make it possible for us to understand your solution without having to run your source code. For full credit, in addition to the algorithm descriptions, your report should include the following.

Part 1 (for everybody):

  1. For every algorithm in 1.1 (DFS, BFS, Greedy, A*) and every one of the three mazes (medium, big, open): give the maze with the computed path, the solution cost, and the number of expanded nodes (12 cases total).
  2. For 1.2, for each of the three mazes (tiny, small, medium): give the solution path, solution cost, and number of expanded nodes for your A* algorithm. Discuss your heuristic, including its admissibility.

Part 2 (for four-credit students):

  1. Discuss your implementation and heuristic. For each of the three inputs (1.1-1.3): give solution paths, number of expanded nodes, running time.
  2. Discuss modifications to your implementation and heuristic. For each of the three inputs (2.1-2.3): give solution paths, number of expanded nodes, running time. For input 2.1 (=1.1), discuss the differences from the previous part.

Extra credit:

  • We reserve the right to give bonus points for any advanced exploration or especially challenging or creative solutions that you implement. Three-credit students can get extra credit for submitting solutions to four-credit problems (point value will be discounted by 50%). If you submit any work for bonus points, be sure it is clearly indicated in your report.

Statement of individual contribution:

  • All group reports need to include a brief summary of which group member was responsible for which parts of the solution and submitted material. We reserve the right to contact group members individually to verify this information.
WARNING: You will not get credit for any solutions that you have obtained, but not included in your report! For example, if your code prints out path cost and number of nodes expanded on each input, but you do not put down the actual numbers in your report, or if you include pictures/files of your output solutions in the zip file but not in your PDF. The only exception is animated paths (videos or animated gifs).

Submission Instructions

By the submission deadline, one designated person from the group will need to upload the following to Compass2g:
  1. A report in PDF format. Be sure to put the names of all the group members at the top of the report, as well as the number of credits (3 or 4). The name of the report file should be lastname_firstname_a1.pdf (based on the name of the designated person).

  2. Your source code compressed to a single ZIP file. The code should be well commented, and it should be easy to see the correspondence between what's in the code and what's in the report. You don't need to include executables or various supporting files (e.g., utility libraries) whose content is irrelevant to the assignment. If we find it necessary to run your code in order to evaluate your solution, we will get in touch with you.

    The name of the code archive should be lastname_firstname_a1.zip.

Compass2g upload instructions:

  1. Log into https://compass2g.illinois.edu and find your section.
  2. Select Assignment 1 (three credits) or Assignment 1 (four credits) from the list, as appropriate.
  3. Upload (1) your PDF report and (2) the zip file containing your code as two attachments.
  4. Hit Submit. -- If you don't hit Submit, we will not receive your submission and it will not count!
Multiple attempts will be allowed but only your last submission before the deadline will be graded. We reserve the right to take off points for not following directions.

Late policy: For every day that your assignment is late, your score gets multiplied by 0.75. The penalty gets saturated after four days, that is, you can still get up to about 32% of the original points by turning in the assignment at all. If you have a compelling reason for not being able to submit the assignment on time and would like to make a special arrangement, you must send me email at least a week before the due date (any genuine emergency situations will be handled on an individual basis).

Be sure to also refer to course policies on academic integrity, etc.